Study design and population
A longitudinal panel design was employed using individual-level data from “Understanding Society: The UK Household Longitudinal Study” [41]. Understanding Society is a rich longitudinal dataset consisting of 10 data collection waves/panels that span from 2009 up to 2020 with around 40,000 households recruited at wave 1 from the four nations of the UK: England, Wales, Scotland, and Northern Ireland. It involves two main surveys: the youth survey which is filled out by young people (aged 10 to 15) and the adult survey which is filled by individuals aged 16 and above [41].
The dataset includes information on the socio-demographic characteristics of individuals (e.g., age, gender, marital status, educational attainment, occupation, housing tenure, perceived financial situation, ethnicity, and country of birth) and on the individuals’ self-reported health, well-being, smoking status, as well as the local authority/council area and census Lower Super Output Areas (LSOAs) where households are located. Individuals recruited in the Understanding Society study are visited each year to collect information on changes to their household and individual circumstances [41].
The sample design of the Understanding Society main survey is made up of four components: 1) the large General Population Sample (around 26,000 recruited households at wave 1, 2009–2010); 2) the Ethnic Minority Boost Sample (around 4000 recruited households at wave 1, 2009–2010); 3) the former British Household Panel Survey sample (at wave 1, 2010); and 4) the Immigrant and Ethnic Minority Boost Sample (around 2,500 recruited households at wave 6, 2015) [41]. Further information on the Understanding Society study design is described elsewhere [42, 43].
For this study, we utilized individual-level data on 67,982 individuals with 404,264 repeated responses (at least 2 repeated responses per individual) across 10 data collection waves over 11 years (2009–2019) from the adult survey (age: 16 +) of the Understanding Society data. It is worth noting that the initial adult survey of the Understanding Society data involved a total of 87,045 individuals with 444,181 repeated responses and that 39,917 observations were deleted due to the reasons summarised in Fig. 1.
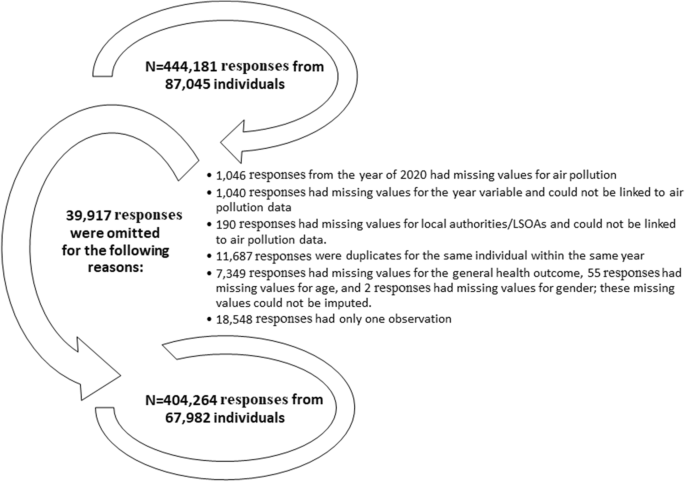
The reasons for omitting survey responses from the UK household longitudinal data
Variables and measurements
Self-reported health
Individuals’ self-reported health which asks how individuals perceive their health in general is assessed on a 5-point Likert scale: 1 = excellent, 2 = very good, 3 = good, 4 = fair, 5 = poor. Out of the total 404,264 general health observations, 105 (0.03%) were missing and were filled out using another health indicator: satisfaction with health, which showed a strong correlation (Pearson’s coefficient = 0.53) with the general health outcome. Satisfaction with health is measured on a 7-point Likert scale (completely satisfied, mostly satisfied, somewhat satisfied, neither satisfied nor dissatisfied, somewhat dissatisfied, mostly dissatisfied, and completely dissatisfied). Therefore, completely satisfied was coded to excellent health, mostly satisfied was coded to very good health, somewhat satisfied was coded to good health, neither satisfied nor dissatisfied and somewhat dissatisfied were coded to fair health, and mostly dissatisfied and completely dissatisfied were coded to poor health.
It should be noted that individuals’ self-reported health was chosen as the main outcome in this study due to its ability to capture the health status from the perspective of the individual and it is considered a reliable measure of health given the high observed correlations between self-reported health and objective health measures (e.g., mortality and hospital admissions) in the literature [11,12,13].
Air pollution
We obtained yearly air pollution data that combine all sources of air pollution including road traffic and industrial/combustion processes for NO2, SO2, PM10, and PM2.5 pollutants from the “Department for Environment Food and Rural Affairs” online database [44]. These are raster data of mean annual concentrations of pollutants measured in µg/m3 up to the year 2019, estimated using air dispersion models at a spatial resolution of 1 × 1 km2, and projected using the UK National Grid [44]. The raster data is projected in a way that each 1 × 1 km2 raster square has the value of a central air pollution point.
For each of the 391 local authorities/council areas in the UK, we computed the average concentration of NO2, SO2, PM10, and PM2.5 pollution from all the centroids of the 1 × 1 km2 raster cells that intersected/fell within the boundaries of the respective local authorities/council areas for each year from 2009 up to 2019. These average concentrations of air pollution were then linked to the “Understanding Society” data using the individuals’ local authority of residence for each year of observation per individual between 2009 and 2019, inclusive.
To minimize exposure bias and establish more robust results, we also linked the 1 × 1 km2 raster air pollution data to the Understanding Society data at the level of Lower Super Output Areas (LSOAs; data zones for Scotland and Super Output Areas for Northern Ireland), a finer geographical scale, for each individual and each year of follow-up (2009–2019). The linkage was done by calculating an area-weighted average air pollution concentration for each LSOA based on the proportion of area intersection between the 1 × 1 km2 raster squares and the respective LSOA. For example, if a LSOA intersected with three 1 × 1 km2 squares in which one intersection covered half of the area of that LSOA while the other two intersections covered a proportion of 0.3 and 0.2, respectively; the air pollution concentration for that LSOA would be 0.5 × air pollution concentration of the first intersected square + 0.3 × air pollution concentration of the second intersected square + 0.2 × air pollution concentration of the third intersected square. Using these smaller spatial units, we conducted our analysis at a smaller geographic scale than local authorities, which allowed us to explore local-contextual patterns of the effect of air pollution on health.
A map showing the local authorities in the UK (council areas in Scotland) and an enlarged subset of 20 local authorities in the southeast of the UK with an example of PM10 concentrations at 1 × 1 km2 grid for the year 2017 for Tower Hamlets local authority and its corresponding LSOAs was used to illustrate the process of air pollution linkages (Fig. 2).
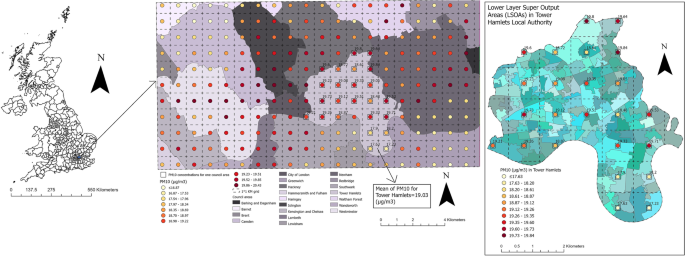
A map showing the local authorities in the UK and an enlarged subset of 20 local authorities in the south-east of the UK with an example of PM10 concentrations at 1 × 1 km2 grid for the year 2017 for Tower Hamlets local authority and its corresponding LSOAs. The green–blue coloured polygons in the LSOAs map represent the LSOAs; The map was constructed by the authors in ArcGIS Pro software using PM10 air pollution shapefile for the year of 2017 downloaded from the DEFRA online data repository [44], local authorities UK boundaries shapefile downloaded from the Office for National Statistics [45], and LSOAs and data zones UK boundaries also downloaded from the Office for National Statistics, National Records of Scotland, and Northern Ireland Statistics [46]. Both DEFRA and Office for National Statistics shapefiles are governed under the Open Government Licence v.3.0
Socio-demographic and lifestyle covariates
In this study, ethnicity (Other-white, Pakistani/Bangladeshi, Indian, Black/African/Caribbean, mixed ethnicities, and other ethnicities versus British-white (Reference category)) and country of birth (non-UK-born and missing information versus UK-born (Reference category)) covariates were considered as effect modifiers in the association between air pollution and self-reported health.
Additionally, we selected a list of individual-level socio-demographic and lifestyle covariates based on what is available in the Understanding Society data and based on the confounders considered by the air pollution-health literature [3, 4]. These included age (coded as 16–18 and then in 5 years increments as 19–23; 24–28; 29–33; 34–38; 39–43; 44–48; 49–53; 54–58; 59–63; 59–63; 64–68; 69–73; 74–78; > 78); gender (females versus males (Reference category)); marital status (living as a couple, single never married, divorced/separated, widowed, and missing information versus married (Reference category)); educational attainment (High school, lower education, other educational qualifications, and still a student versus university degree (Reference category)); occupation (Non-manual workers, manual workers, student/retired/not-working and missing information versus managers/professionals/ employers (Reference category)); housing tenure (Owned with mortgage, local authority rent, housing association rent, private rent and other or missing information versus owned outright (Reference category)); perceived financial situation (living difficultly and missing information versus living comfortably/doing alright (Reference category)); and smoking (smoker and missing information versus non-smoker (Reference category)) [47].
The question about smoking was not asked during wave 1 of data collection and during waves 3 and 4 for people above the age of 21 years old. Therefore, individual responses on smoking from wave 2 were used as a proxy for the smoking status in waves 1, 3, and 4 [47]. This imputation is unlikely to deviate from the real smoking status scenario because the intraclass correlation coefficient (ICC) indicates a 97% similarity in the individual smoking responses across the data collection waves.
Finally, year dummies (calendar year: 2009–2019) were considered as a control for the time trend in our analysis following the approach of relevant studies [48, 49]. Given that our study utilises yearly air pollution data, controlling for other temporal covariates considered by relevant literature such as seasonal trends [50, 51] was not possible.
Data analysis
Percentages were computed to describe the individuals’ socio-demographic and lifestyle factors for each wave (waves 1 to 10) of the Understanding Society sample. We also examined the correlation between NO2, SO2, PM10, and PM2.5 pollutants at the two geographical scales of local authorities and LSOAs using Pearson’s correlation coefficient. Given the high observed correlations between the pollutants (Pearson’s coefficient ≥ 0.7 [52]; Tables 2 and 3), the association of NO2, SO2, PM10, and PM2.5 pollutants with self-reported health was examined in separate regression models. However, a low to moderate correlation was observed between SO2 and each of the other three pollutants, which enabled the construction of bi-pollutant models adjusting the NO2, PM10, and PM2.5 models for the SO2 pollutant.
Intraclass correlation coefficients (ICCs) were computed to assess the homogeneity in the self-reported general health responses within individuals and household clusters. An ICC of more than 0.3 indicates the presence of fair to high homogeneity in the responses within the examined clusters across time [53]. Given the presence of 65% homogeneity (ICC = 0.65; Table 4) within the responses of self-reported health for each individual across time, the mean of self-reported health was calculated from predictions of mixed-effects linear models, which were adjusted for age in fixed effects and for the individual ID in the random intercept.
Three-level (repeated individual observations across time nested within local authorities or LSOAs) mixed-effects ordered logistic models were used to assess the association between self-reported general health and each of NO2, SO2, PM10, and PM2.5 pollutants. Mixed-effects ordered logistic models were used to account for the nested-longitudinal structure of the data and because general health is an ordinal outcome, which is measured on a 5-point (Excellent, very good, good, fair, and poor health) Likert scale. These models were adjusted for the socio-demographic and lifestyle covariates and the year (2009–2019) dummies. The models which involve air pollution linked at the LSOAs level were additionally adjusted for the LSOAs population density. This was done to account for any bias introduced by the LSOAs being constructed by dividing areas in the four nations of the UK based on the population size. In a supplementary analysis, we also demonstrate the association of self-reported health with each of the socio-demographic and lifestyle covariates (Additional file 1: Supplementary Table 1). It is worth noting that we did not account for the household clustering in the random intercept of the mixed-effects ordered logistic models due to the low observed homogeneity in the self-reported health responses within each household cluster (ICC = 0.24; Table 4).
In further analysis, we decomposed the overall effect of air pollution (linked at the local authority or LSOAs level) on health into between (spatial) and within (temporal) effects. Between effects (Eq. 1) were used to determine the spatial effect of air pollution by computing the mean of air pollution across the 11 years of follow-up (2009–2019) for each local authority and each LSOA. On the contrary, within effects (Eq. 2) were used to determine the temporal effect of air pollution by calculating the yearly air pollution deviation from the 11 years mean for each local authority and LSOA. The multilevel mixed-effects ordered logistic models were used to examine the overall (Eq. 3) effect of air pollution as well as the between and within effects (Eq. 4) of air pollution on self-reported health at two geographical scales (coarse local authorities and detailed LSOAs).
Finally, we incorporated into the mixed-effects models an interaction term between ethnicity and each of NO2, SO2, PM10, and PM2.5 pollutants and between country of birth and each of the four pollutants to assess whether the association between air pollution and health varies between ethnic groups and by country of birth. Interaction terms were incorporated into the overall pollutant models (Eqs. 5 and 6) and into the between-within models, each at a time. Coefficient plots were used to visualize the interaction analysis results.
$${\text{Between pollutant concentration}}_{\text{tij}}=\overline{{\text{overall pollutant concentration} }_{\text{j}}}$$
(1)
$${\text{Within pollutant concentration}}_{\text{tij}}={|\text{overall pollutant concentration}}_{\text{tj}}-\overline{{\text{ overall pollutant concentration} }_{\text{j}}}|.$$
(2)
Where i is the individual; t is the time in years; and j is the local authority or LSOA.
$$\mathit{ln}\left(\frac{{Y}_{\mathit{ctij}}}{1-{Y}_{\mathit{ctij}}}\right)={\beta }_{c} + {U}_{cij}+{U}_{cj} + {\beta 1\text{overall pollutant concentration}}_{tij}+ {\beta 2\text{Age}}_{tij}+ {\beta 3\text{Gender}}_{tij}+ {\beta 4\text{Ethnicity}}_{tij}+ {\beta 5\text{Country of birth}}_{tij}+ {\beta 6\text{Marital status}}_{tij}+ {\beta 7\text{Education}}_{tij}+{\beta 8\text{Occupation}}_{tij}+{\beta 9\text{Housing tenure}}_{tij}+ {\beta 10\text{Perceivedfinancial situation}}_{tij}+ {\beta 11\text{Smoking status}}_{tij}+ {\beta 12\text{Year dummies}}_{ij}+ {\varepsilon }_{tij}$$
(3)
$$\mathit{ln}\left(\frac{{Y}_{\mathit{ctij}}}{1-{Y}_{\mathit{ctij}}}\right)={\beta }_{c} + {U}_{cij}+{U}_{cj} + {\beta 1\text{Between pollutant concentration}}_{tij}+ {\beta 2\text{Within pollutant concentration}}_{tij}+ {\beta 3\text{Age}}_{tij}+ {\beta 4\text{Gender}}_{tij}+ {\beta 5\text{Ethnicity}}_{tij}+ {\beta 6\text{Country of birth}}_{tij}+ {\beta 7\text{Marital status}}_{tij}+ {\beta 8\text{Education}}_{tij}+ {\beta 9\text{Occupation}}_{tij}+ {\beta 10\text{Housing tenure}}_{tij}+ {\beta 11\text{Perceived financial situation}}_{tij}+ {\beta 12\text{Smoking status}}_{tij}+ {\beta 13\text{Year dummies}}_{ij} + {\varepsilon }_{tij}$$
(4)
$$\mathit{ln}\left(\frac{{Y}_{\mathit{ctij}}}{1-{Y}_{\mathit{ctij}}}\right)={\beta }_{c} + {U}_{cij}+{U}_{cj} + \beta 1\text{overall pollutant concentration}\times {\text{Ethnicity}}_{tij} + {\beta 4\text{Age}}_{tij}+ {\beta 5\text{Gender}}_{tij}+ {\beta 6\text{Country of birth}}_{tij}+ {\beta 7\text{Marital status}}_{tij}+ {\beta 8\text{Education}}_{tij}+ {\beta 9\text{Occupation}}_{tij}+ {\beta 10\text{Housing tenure}}_{tij}+ {\beta 11\text{Perceivedfinancial situation}}_{tij}+ {\beta 12\mathrm{Smoking status}}_{tij}+ {\beta 13\mathrm{Year dummies}}_{ij} + {\varepsilon }_{tij}$$
(5)
$$\mathit{ln}\left(\frac{{Y}_{\mathit{ctij}}}{1-{Y}_{\mathit{ctij}}}\right)={\beta }_{c} + {U}_{cij}+{U}_{cj} + \beta 1\text{overall pollutant concentration}\times {\text{Country of birth}}_{tij} + {\beta 4\text{Age}}_{tij}+ {\beta 5\text{Gender}}_{tij}+ {\beta 6\text{Ethnicity}}_{tij}+ {\beta 7\text{Marital status}}_{tij}+ {\beta 8\text{Education}}_{tij}+ {\beta 9\text{Occupation}}_{tij}+ {{\beta 10\text{Housing tenure}}_{tij}+ \beta 11\text{Perceivedfinancial situation}}_{tij}+ {\beta 12\text{Smoking status}}_{tij}+ {\beta 13\text{Year dummies}}_{ij} + {\varepsilon }_{tij}$$
(6)
where Yctij is the health outcome for individual i measured using 5 ordered categories (c = 1, 2, 3, 4, 5), in local authority or LSOA j at year t; β1, β2 …. β12 are the slopes of fixed effects; βc is the fixed intercept for the 5 ordered categories (c = 1, 2, 3, 4, 5); Ucij is level 2 random intercept of individuals nested in local authorities or LSOAs for the 5 ordered categories (c = 1, 2, 3, 4, 5); Ucj is level 3 random intercept of local authorities or LSOAs for the 5 ordered categories (c = 1, 2, 3, 4, 5); εtij are the model residuals; Models involving air pollution linked at the LSOAs level are additionally adjusted for the LSOAs population density.
In a sensitivity analysis, we performed the same multilevel mixed-effects ordered logistic models to examine the overall and the between-within effects of air pollution (linked at the level of local authority and LSOAs) on self-reported health and how these effects vary by ethnic groups and country of birth only for individuals recruited in wave 1 of the Understanding Society data. This sensitivity analysis was carried out to balance the cohort effect because not all individuals in our sample were recruited in wave 1 and attrition bias is more probable at later waves.
In a sensitivity analysis, we also carried out four-level mixed-effects logistic models with repeated individual responses nested in LSOAs, nested in local authorities to examine the association between air pollution linked at the LSOAs level and self-reported general health coded as a binary variable of fair/poor health versus excellent/very good/good health. This sensitivity analysis was conducted to assess in more details the local and regional effects of air pollution on health in the general population and by ethnicity. Given the complexity of the four-level nested models, the analysis was performed using a binary version of the general health outcome rather than the ordered Likert scale version.
Statistical analysis was conducted using STATA software (StataCorp. 2015. Stata Statistical Software: Release 14. College Station, TX: StataCorp LP) and spatial pre-processing was conducted using ArcGIS Pro software. Regression results were reported in terms of odds ratios (ORs) and 95% confidence intervals (CIs) per 10 µg/m3 increase in air pollution. Statistical significance was considered at a P-value of less than 0.05.
